 |
| Mathematik |
| Fachoberschule - Technik |
|
 |
| Extremwertaufgaben |
|
|
|
| Lösungsalgorithmus |
|
| |
|
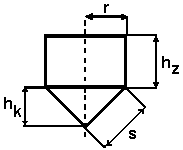
Beispiel:
Ein Wasserbehälter hat die Form eines Kreiszylinders mit unten angesetztem geraden Kreiskegel.
Die Höhe hZ des Kreiskegels soll 2 m, die Mantellinie s des Kegels 6 m betragen.
Welche Abmessungen muß der Behälter bei größtem Fassungsvermögen haben? |
| 1. |
Stelle das Problem - wenn möglich -
an Hand einer Skizze dar!
Kennzeichne die gegebenen und die gesuchten Größen! |
Lösung:
Skizze: |
 |
| | 2. |
Gib die Größe an, die extrem werden soll! |
V --> maximal |
| 3. |
Formuliere einen mathematischen Zusammenhang zwischen der extrem werden Größe und den anderen Angaben! Ggf. enthält diese Gleichung mehr als eine Variable! |
V ( r, hk ) =   r2 hz + r2 hz + |
|
  r2 hk r2 hk |
|
| 4. |
Suche / Finde Nebenbedingungen!
Verknüpfe bekannte mit unbekannten Größen! |
| Nebenbedingung: |
Nach dem Lehrsatz des PYTHAGORAS gilt: |
| |
r2 = 36 - hk2 |
|
| 5. |
Ersetze die Variablen durch die Nebenbedingungen! - Somit ist die extrementale Größe nur noch von einer Variablen abhängig. |
| V ( hk ) = |
|
  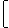
| 6 |  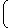 | 36 - | hk2 | 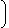 | - | 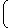 | 36hk - | hk3 | 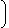 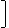 |
|
| 6. |
Denke über den Definitionsbereich nach! |
| Definitionsbereich: |
0 < hk < 6 |
|
| 7. |
Bilde die 1. und 2. Ableitung! |
| V' ( hk ) = |
|
  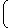 | 36 - | 3hk2 - 12hk | 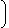 |
und |
| V'' ( hk ) = |
|
  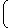 | -6hk - 12 | 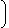 |
| | 8. |
Berechne die Nullstelle(n) der 1. Ableitung und vergleiche mit dem Definitionsbereich! |
Als Nullstellen der 1. Ableitung erhält man
| hk1 = 2 |
und |
hk2 = -6  DB DB |
| | 9. |
Weise mit Hilfe der 2. Ableitung das Extremum nach! |
Die 2. Ableitung wird für h = 2 negativ, somit ist ein Maximum nachgewiesen.
Die Abmessungen des Behälters betragen somit
| hk = 2m |
und |
r = 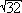 m m |
| | 10. |
Berechne - wenn gefordert - den Extremwert! |
|
|
|
| Extremwertaufgaben |
| 1 |
 |
|
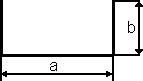 Aus Blechtafeln von je 1m Breite soll ein rechteckiger Warmluftkanal gebogen werden ( siehe Skizze ).
Aus Blechtafeln von je 1m Breite soll ein rechteckiger Warmluftkanal gebogen werden ( siehe Skizze ).
Wie müssen die Maße sein, damit möglichst viel Luft transportiert werden kann?
|
| 1 |
 |
|
| 2 |
 |
|
Die Zahl 100 soll so in zwei Summanden zerlegt werden, daß die Summe der Quadrate der beiden Summanden möglichst klein wird.
|
| 2 |
 |
|
| 3 |
 |
|
Ein Rechteck mit dem Umfang u rotiere um eine seiner Mittelachsen, so daß ein Zylinder entsteht.
Welche Maße muß das Rechteck besitzen, damit das Zylindervolumen ein Maximum annimmt?
|
| 3 |
 |
|
| 4 |
 |
|
Einem gleichseitigen Dreieck mit der Seitenlänge a = 1LE soll ein Rechteck mit möglichst großem Flächeninhalt einbeschrieben werden, und zwar so, daß eine Rechteckseite auf einer Dreieckseite liegt.
Die Rechteckseiten sind zu berechnen!
|
| 4 |
 |
|
| 5 |
 |
|
Welcher Punkt des Graphen von f:
| f(x) = |
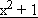 |
| x |
|
; x > 0 liegt dem Koordinatenursprung am nächsten?
|
|
| 5 |
 |
|
| 6 |
 |
|
In eine Kugel mit dem Radius R wird ein Kegel einbeschrieben...
Wie hoch ist der Kegel mit maximalem Volumen? |
| 6 |
 |
|
| 7 |
 |
|
Eine Wasserstraße führt von einem Anlegeplatz A nahezu geradlinig zum Hafen H. Eine Lagerhalle L liegt im rechten Winkel zu AH seitlich von A. Die Entfernungen AH sind 80 km, AL 40 km.
Der Transport von Waren auf dem Landweg sind fünf Mal so teuer wie auf dem Wasserweg.
Wo wird man von L nach H zu transportierende Frachten auf Kähne verladen, damit die gesamten Transportkosten minimal werden? |
| 7 |
 |
|
| 8 |
 |
|
Zwei OHMsche Widerstände R1 und R2 ergeben bei Parallelschaltung einen Gesamtwiderstand von 160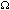 .
In Reihenschaltung soll ihr Gesamtwiderstand minimal sein. Berechnen Sie R1 und R2! .
In Reihenschaltung soll ihr Gesamtwiderstand minimal sein. Berechnen Sie R1 und R2! |
| 8 |
 |
|
| 9 |
 |
|
Ein Land in Mittelamerika kann x Tonnen Kaffee pro Monat verkaufen. Der Preis, der dafür auf dem Weltmarkt zu erzielen ist,
| beträgt |
 |
600 - |
|
 |
DM je Tonne. Für das Verschiffen von x Tonnen Kaffee müssen 2500 DM feste |
Kosten und zusätzlich 45 DM je Tonne bezahlt werden.
Wieviel Tonnen Kaffee müssen expotiert werden, damit das Land die größtmöglichen Einnahmen dafür erzielt?
|
| 9 |
 |
|
| 10 |
 |
|
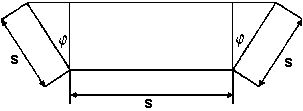 Ein Kanal soll den in der Abbildung dargestellten Querschnitt mit bekanntem s haben.
Ein Kanal soll den in der Abbildung dargestellten Querschnitt mit bekanntem s haben.
Wie muß der Winkel 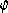 gewählt werden, damit die Querschnittsfläche maximal wird? gewählt werden, damit die Querschnittsfläche maximal wird? |
| 10 |
 |
|
| |