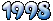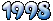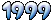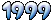|
| Mathematik |
| Fachoberschule - Technik |
|
 |
|
Prüfungen
|
|
| Prüfungshinweise für den Lehrer |
|
| 1. |
Den Schülern ist für die Arbeit das erforderliche Papier (mit Schulstempel versehen) zur Verfügung zu stellen. |
| 2. |
Vor Beginn der Prüfung ist ihnen (Schülern) mitzuteilen: |
| |
| - Die Arbeitszeit beträgt 210 Minuten (einschließlich Einlesezeit)! |
- Es sind folgende Hilfsmittel zugelassen
| - Für die Schule gültige Tafelwerke / Formelsammlungen |
| - Zeichengeräte |
| - Nichtprogrammierbare, nichtgraphikfähige Taschenrechner |
| - Duden |
| |
| 3. |
Es werden nur ganze Punkte erteilt. Für richtig vollzogene Teilschritte, in die falsche Zwischenergebnisse eingegangen sind, wird die vorgesehene Punktzahl erteilt, jedoch ist bei sinnlosem Endergebnis mindestens ein Punkt abzuziehen. Die vorgesehene Punktzahl wird nicht erteilt, wenn sich diese Teilschritte durch vorher begangene Fehler wesentlich vereinfachen. |
| 4. |
Der Lösungsweg muss übersichtlich gegliedert, sauber und durchschaubar dargestellt sein. |
| 5. |
Löst der Schüler beide Wahlaufgaben, so wird die Aufgabe gewertet, bei deren Lösung die höhere Punktzahl erreicht wurde.
Ein Zusatzpunkt wird erteilt, wenn der Schüler beide Wahlaufgaben richtig gelöst hat. |
| 6. |
Die Bewertungseinheiten für die Aufgaben bzw. für deren Teilschritte sind der Aufgabenstellung zu entnehmen. |
| 7. |
Aus der graphischen Darstellung sollen die markanten Punkte deutlich erkennbar sein. Das Zeichnen mit Kurvenschablonen wird nicht verlangt. |
| 8. |
Die numerischen Ergebnisse in den Lösungshinweisen sind häufig gerundete Werte. |
| 9. |
Bewertungsmaßstab:
| 47 |
- |
50 Punkte |
Note 1 |
| 39 |
- |
46 Punkte |
Note 2 |
| 31 |
- |
38 Punkte |
Note 3 |
| 22 |
- |
30 Punkte |
Note 4 |
| 12 |
- |
21 Punkte |
Note 5 |
| 00 |
- |
11 Punkte |
Note 6 |
|
|
| Prüfung |

|
| Pflichtaufgaben |
| 1 |
Der Punkt P(1;-9) ist Wendepunkt einer ganzrationalen Funktion dritten Grades y = f(x).
Die Gerade t mit y = t(x) = -9x+2 ist Tangente an den Graph der Funktion f im Punkt N(0;2). |
| 1.1 |
Berechnen Sie die Koeffizienten der Funktionsgleichung von f!
(Ergebnis y = f(x) = x3-3x2-9x+2) |
| 1.2 |
Ermitteln Sie die Nullstellen und die lokalen Extrempunkte von f! |
| 1.3 |
Skizzieren Sie den Graph von f im Intervall [ -2,5 ; 5 ] und geben Sie die Monotonieintervalle an! |
| 1.4 |
Die Tangente t und der Graph von f schließen ein Flächenstück vollständig ein.
Berechnen Sie dessen Flächeninhalt! |
| 2 |
Ein Trichter hat die Form eines oben offenen geraden Kreiskegels. Welchen Radius r und welche Höhe h muss der Trichter haben, damit sein Fassungsvermögen bei einer Mantellinie von 10 cm Länge möglichst groß wird?
Berechnen Sie das maximale Volumen! |
| Wahlaufgaben (Von diesen Aufgaben muß nur eine gelöst werden) |
| 3 |
Es sind die Gleichungen der Geraden g1 und g2 gegeben:
| g1: |
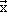 = ( -3 ; 3 ; 9 ) = ( -3 ; 3 ; 9 ) |
+ r ( -2 ; 3 ; 5 ) |
| g2: |
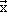 = ( -1 ; -10 ; -2 ) = ( -1 ; -10 ; -2 ) |
+ s ( 2 ; 7 ; 1 ) |
|
| 3.1 |
Der Schnittpunkt der beiden Geraden g1 und g2 ist der Dreieckspunkt A.
Berechnen Sie seine Koordinaten ! |
| 3.2 |
Vom Dreieckspunkt B ist folgendes bekannt:
B  g2 und xB = 3. Berechnen Sie die übrigen Koordinaten von B! g2 und xB = 3. Berechnen Sie die übrigen Koordinaten von B! |
| 3.3 |
Weisen Sie nach, dass der Dreieckspunkt C ( -1 ; 0 ; 4 ) auf der Geraden g1 liegt! |
| 3.4 |
Geben Sie eine Gleichung der Geraden g3 an, die durch die Punkte B und C geht! |
| 3.5 |
Berechnen Sie den Winkel  = = 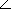 (CAB) und den Flächeninhalt des Dreiecks ABC! (CAB) und den Flächeninhalt des Dreiecks ABC! |
| 3.6 |
| Für welchen Punkt Q der Geraden g3 durch B, C gilt |
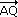 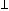  | ? |
Geben Sie die Koordinaten von Q an ! |
| 4 |
Die in der Zeit t gelöste Masse fester Substanzen in wässrigen Lösungen wird durch die
Funktion m = mO ( 1 - ekt ) beschrieben.
Hierbei sind mO die Sättigungsmenge und k eine vom Stoff abhängige Konstante. |
| 4.1 |
Bei einem Versuch, für den k1 = 0,20 min-1 gilt, wird festgestellt, dass 20g der Substanz in
der ersten Minute in Lösung gegangen sind. Berechnen Sie die Sättigungsmasse mO! |
| 4.2 |
Für eine andere Substanz gilt: mO = 200 g, k2 = 0,17 min-1.
Nach welcher Zeit sind 120 g dieser Substanz in Lösung gegangen? |
| 4.3 |
Bei einer weiteren Substanz ist nach 5,0 min die Hälfte der entsprechenden Sättigungsmenge in Lösung gegangen. Berechnen Sie k3! |
| 4.4 |
Untersuchen Sie die Funktion m(t) = mO ( 1 - e-kt ) auf Nullstellen! |
| 4.5 |
Bestimmen Sie von der Funktion m(t) = 4 ( 1 - e-0,5 t ) den Anstiegswinkel der Tangente im Punkt P ( 2 ; m(2)) und skizzieren Sie m(t) im Intervall [ 0 ; 4 ]! |
 |
|
|
 |
| Prüfung |
 |
| Pflichtaufgaben |
| 1 |
Gegeben ist die Funktion f mit y = f(x) = -0,25x4 + 0,5x2 + 2. |
| 1.1 |
Zeigen Sie, dass der Graph der Funktion f achsensymmetrisch zur y - Achse ist! |
| 1.2 |
Berechnen Sie die Nullstellen, die Extrempunkte (einschließlich Nachweise) und die Wendepunkte (einschließlich Nachweise) der Funktion f. |
| 1.3 |
Zeichnen Sie den Graph der Funktion f im Intervall -2,5 ≤ x ≤ 2,5 ( 1 LE = 2cm )! |
| 1.4 |
Zeichnen Sie die Wendetangenten ein und berechnen Sie dann den Winkel, unter dem sich die Wendetangenten schneiden! |
| 2 |
Zur Fertigung eines Hohlkegels wird aus einer kreisförmigen Scheibe vom Radius R=6dm ein Sektor herausgeschnitten und an den Schnittkanten zusammengeheftet. Dabei soll das Volumen des Kegels maximal werden. |
| 2.1 |
Stellen Sie das Volumen des Kegels als Funktion seiner Höhe h dar!
(die Blechdicke wird vernachlässigt) |
| 2.2 |
Errechnen Sie die Höhe des Kegels für den Fall, daß sein Volumen maximal wird!
(einschließlich Nachweis des Extremums) |
| 2.3 |
In welchem Verhältnis stehen Höhe h und Radius des Kegels r zueinander? |
| 3 |
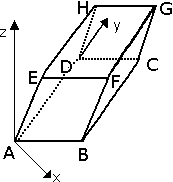 Das Raumgitter eines Kristalls habe die Form eines schrägen, vierseitigen Prismas ABCDEFGH. (siehe Skizze rechts)
Das Raumgitter eines Kristalls habe die Form eines schrägen, vierseitigen Prismas ABCDEFGH. (siehe Skizze rechts)
Durch die Wahl des skizzierten Koordinatensystems läßt sich das Raumgitter durch folgende Vektoren aufspannen:
|
| 3.1 |
Bestimmen Sie die Koordinaten aller übrigen Eckpunkte des Prismas, wenn A ( 0 ; 0 ; 0 ) gilt! |
| 3.2 |
Berechnen Sie den Neigungswinkel der Seitenkante 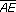 des Prismas zur Grundfläche ABCD! des Prismas zur Grundfläche ABCD! |
| 3.3 |
Die Raumdiagonale 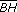 und und 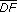 schneiden sich im Punkt P. schneiden sich im Punkt P.
Berechnen Sie seine Koordinaten und den Winkel, unter dem sich die Raumdiagonalen schneiden! |
| 3.4 |
Zeigen Sie, dass zwei der vier Raumdiagonalen gleich lang sind und sich die Maßzahlen der beiden anderen wie 1 : 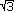 verhalten! verhalten! |
 |
|
|
 |
| Prüfung |
 |
| Pflichtaufgaben |
| 1 |
Gegeben sei die Funktion f mit der Gleichung
y = f(x) = ( -x2 + 2x + 3 )  (x - 1 ) = -x3 + 3x2 + x - 3. (x - 1 ) = -x3 + 3x2 + x - 3. |
| 1.1 |
Bestätigen Sie, dass die Funktion f für alle x  R weder achsensymmetrisch zur y - Achse noch punktsymmetrisch zum Punkt P ( 0 ; 0 ) ist! R weder achsensymmetrisch zur y - Achse noch punktsymmetrisch zum Punkt P ( 0 ; 0 ) ist! |
| 1.2 |
Berechnen Sie die Nullstellen dieser Funktion! |
| 1.3 |
Ermitteln Sie die Koordinaten der Extrempunkte und weisen Sie deren Art nach! |
| 1.4 |
Ermitteln Sie die Koordinaten des Wendepunktes! |
| 1.5 |
Untersuchen Sie das Verhalten der Funktion f für x --> ± ∞. |
| 1.6 |
Skizzieren Sie den Graph der Funktion f im Intervall -1,5 ≤ x ≤ 3,5 ( 1 LE = 1cm )! |
| 1.7 |
Im I.Quadrant begrenzen der Graph der Funktion f und die x - Achse eine Fläche vollständig. Berechnen Sie den Inhalt dieser Fläche! |
| 2 |
Eine Strecke der Länge l wird in zwei Teilstücke zerlegt. Das eine Teilstück wird als Seite a eines Quadrates, das andere als Radius r eines Kreises benutzt. |
| 2.1 |
Ermitteln Sie die Seite a und den Radius r als Funktion der Länge l für den Fall, daß die Summe der Flächeninhalte ein Minimum wird. Wie verhält sich der Radius r zur Seite a des Quadrates? |
| 2.2 |
Ermitteln Sie den Radius r und die Seitenlänge a für l = 10 dm!
Geben Sie dann den minimalen Flächeninhalt an! |
| Wahlaufgaben (Von diesen Aufgaben muß nur eine gelöst werden) |
| 3 |
| Gegeben sei die Funktion f mit der Gleichung |
y = f(x) = |
|
. |
|
| 3.1 |
Geben Sie den Definitionsbereich der Funktion f an! |
| 3.2 |
Bilden Sie die 1.Ableitung der Funktion f!
Zeigen Sie, dass die Funktion f keine Extrema besitzt! |
| 3.3 |
Untersuchen Sie die Funktion f mit Hilfe der 1.Ableitung auf Monotonie! |
| 3.4 |
|
| 3.5 |
Berechnen Sie die Koordinaten des Wendepunktes und stellen Sie eine Gleichung für die Wendetangente auf! (Verzicht auf die 3. Ableitung) |
| 3.6 |
Zeichnen Sie den Graph der Funktion f im Intervall -2 ≤ x ≤ 4 ( 1 LE = 2cm )! |
| 4 |
Es sei ein Dreieck im kartesischen Koordinatensystem durch die Eckpunkte
A ( -5 ; -1 ), B ( 3 ; -2 ) und C ( -3 ; 8 ) gegeben. |
| 4.1 |
Berechnen Sie die Länge der Seite b =  ! ! |
| 4.2 |
Geben Sie eine Gleichung der Geraden, die durch die Punkte A und C festgelegt ist, in Parameterform und in parameterfreier Form (y = mx + n) an! |
| 4.3 |
Der Schnittpunkt der Seitenhalbierenden mit der Seite b sei D! Geben Sie eine Gleichung der Geraden in parameterfreier Form an, die die Seitenhalbierende der Seite b enthält! |
| 4.4 |
Bestimmen Sie den Winkel zwischen der Seitenhalbierenden von b und der Seite b! |
| 4.5 |
Ermitteln Sie den Flächeninhalt des Dreiecks ADB! |
 |
|
|
 |
| Prüfung |
 |
| Pflichtaufgaben |
| 1 |
Gegeben ist die Funktion f mit y = f(x) = x3 - 6x2 + 9x x  R! R! |
| 1.1 |
Berechnen Sie Nullstellen, Hoch-, Tief- und Wendepunkte dieser Funktion! (einschließlich Nachweise) |
| 1.2 |
Zeichnen Sie den Graph von f im Intervall [0;4] ! |
| 1.3 |
Der Graph von f und die x - Achse schließen eine Fläche vollständig ein.
Berechnen Sie deren Inhalt! |
| 1.4 |
Gegeben ist die Parabel p mit der Gleichung y = p(x) = 0,5x2 - 2x + 4 x  R R |
| 1.4.1 |
Bestimmen Sie die Koordinaten ihres Scheitels! |
| 1.4.2 |
Zeichnen Sie die Parabel in das Koordinatensystem von 1.2 ein! (Intervall [0;4]) |
| 1.4.3 |
Ermitteln Sie die Schnittpunkte der Geraden von f und p |
| 2 |
Ein Quader besitzt die Höhe h, eine quadratische Grundfläche mit der Seitenlänge a und ein Volumen von 2000 cm³. Aus Kostengründen ist die Oberfläche zu minimieren. |
| 2.1 |
Berechnen Sie die minimale Oberfläche! (einschließlich Nachweis des Minimums) |
| 2.2 |
In welchem Verhältnis stehen für diesen Fall a und h zueinander? |
| Wahlaufgaben (Von diesen Aufgaben muß nur eine gelöst werden) |
| 3 |
Die Funktion f mit y = f(t) = 2e-t cos(t) 0 ≤ t ≤ 2 beschreibt die Elongation eines Federschwingers in Abhängigkeit von der Zeit. beschreibt die Elongation eines Federschwingers in Abhängigkeit von der Zeit. |
| 3.1 |
Berechnen Sie die Zeiten t, für die die Elongation im betrachteten Intervall Null ist! |
| 3.2 |
Im vorgegebenen Intervall besitzt die Funktion lokale Extrema.
Berechnen Sie diese und weisen Sie deren Art nach! |
| 3.3 |
Skizzieren Sie den Graph von f im Intervall 0 ≤ t ≤ 2 ! !
(zu wählende Einheiten: t - Achse : 1 LE = 1cm / y - Achse : 1 LE = 10cm) |
| 3.4 |
Geben Sie für die Funktion f für das Intervall 0 ≤ t ≤ 2 den Wertebereich an! den Wertebereich an! |
| 4 |
Es sein die Geraden g und h gegeben.
Die Gerade g werde durch den Punkt B ( -1 ; -2 ; -3 ) und den Richtungsvektor  = 2 = 2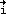 + 4 + 4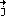 + 6 + 6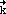 beschrieben, die Gerade h sei durch die Punkte C ( 5 ; 2 ; 1 ) und E ( 3 ; 2 ; 2 ) festgelegt. beschrieben, die Gerade h sei durch die Punkte C ( 5 ; 2 ; 1 ) und E ( 3 ; 2 ; 2 ) festgelegt. |
| 4.1 |
Stellen Sie eine Gleichung in Parameterform für g und h auf! |
| 4.2 |
Die Geraden g und h schneiden einander im Punkt A. Berechnen Sie seine Koordinaten! |
| 4.3 |
Die Punkte A, B und C bilden ein Dreieck.
Berechnen Sie den Winkel 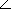 ABC und den Flächeninhalt dieses Dreiecks! ABC und den Flächeninhalt dieses Dreiecks! |
| 4.4 |
Die Vektoren 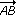 und und 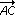 spannen ein Parallelogramm ABCD auf. spannen ein Parallelogramm ABCD auf.
Ermitteln Sie die Koordinaten von D! |
 |
|
|
 |
| Prüfung |
 |
| Pflichtaufgaben |
| 1 |
| Gegeben sei die Funktion f mit |
y = f(x) = |
|
. |
|
| 1.1 |
Für welchen x - Wert ist die Funktion f nicht definiert?
Welche Art der Unstetigkeit (Unterbrechung) liegt vor? |
| 1.2 |
Zeichnen Sie den Graph von f im Intervall [ 0,9 ; 5 ]! |
| 1.3 |
Berechnen Sie, ab welcher reellen Zahl x des Intervalls [0,9;5] alle Funktionswerte kleiner 1 sind! |
| 1.4 |
Weisen Sie nach, daß die Funktion f keine lokalen Extrema besitzt! |
| 1.5 |
Die Tangente im Punkt P0 ( x0 ; y0 ) mit x0  [ 0,9 ; 5 ] an den Graph der Funktion f hat den [ 0,9 ; 5 ] an den Graph der Funktion f hat den
Berechnen Sie die Koordinaten von P0 und stellen Sie eine Gleichung für diese Tangente auf! |
| 1.6 |
Berechnen Sie den Inhalt der Fläche zwischen der Kurve von f und der x - Achse im
Intervall [ 1 ; 4 ]! |
| 2 |
Ermitteln Sie die Koordinaten des Endpunktes des Vektors, der im Punkt P1 ( -2 ; 3 ; 5 ) angreift, in Richtung auf P2 ( 6 ; -1 ; 2 ) zeigt und die Länge s = 31,5 besitzt! |
| Wahlaufgaben (Von diesen Aufgaben muß nur eine gelöst werden) |
| 3 |
Gegeben ist die Funktion f mit y = f(x) = ( x - 3 )  e0,5x. e0,5x. |
| 3.1 |
Berechnen Sie die Schnittpunkte des Graphen von f mit den Koordinatenachsen und untersuchen Sie das Verhalten der Funktion f für x --> ± ∞! |
| 3.2 |
Bestimmen Sie Extrem- und Wendepunkte! (einschließlich Nachweise) |
| 3.3 |
Zeichnen Sie den Graph der Funktion f im Intervall [ -2 ; 4 ]! |
| 3.4 |
Weisen Sie nach, dass die Funktion F mit y = F(x) = ( 2x - 10 )  e0,5x eine Stammfunktion der gegebenen Funktion f ist! e0,5x eine Stammfunktion der gegebenen Funktion f ist! |
| 3.5 |
Berechnen Sie den Inhalt der Fläche, die von den Koordinatenachsen und der Kurve der gegebenen Funktion f vollständig eingeschlossen wird! |
| 4 |
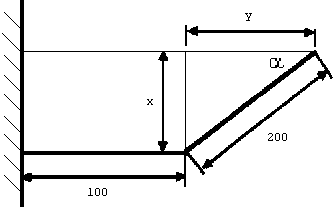 Eine Blechtafel von 300mm Breite wird bei 100mm so abgewinkelt, dass sie an einer Wand als Rinne mit möglichst großem trapezförmigen Querschnitt angebracht werden kann.
Eine Blechtafel von 300mm Breite wird bei 100mm so abgewinkelt, dass sie an einer Wand als Rinne mit möglichst großem trapezförmigen Querschnitt angebracht werden kann.
(siehe Skizze, nicht maßstäblich!) |
| 4.1 |
Stellen Sie die Strecken x und y in Abhängigkeit des Winkels  dar! dar! |
| 4.2 |
Geben Sie eine Formel zur Berechnung der trapezförmigen Querschnittsfläche in Abhängigkeit des Winkels  an! an! |
| 4.3 |
Ermitteln Sie den Winkel  so, dass die Querschnittsfläche maximal wird! so, dass die Querschnittsfläche maximal wird!
(Auf den Nachweis des Extremums wird verzichtet!) |
 |
|
|
 |
| Prüfung |
 |
| Pflichtaufgaben |
| 1 |
| Gegeben ist die Funktion f mit |
y = f(x) = |
|
. |
|
| 1.1 |
Berechnen Sie die Unstetigkeitsstelle und geben Sie deren Art an! |
| 1.2 |
Überprüfen Sie durch Rechnung, ob der Graph von f Schnittpunkte mit den Koordinatenachsen besitzt! |
| 1.3 |
Die Funktion f hat je einen lokalen Maximumpunkt und einen lokalen Minimumpunkt.
Berechnen Sie deren Koordinaten! |
| 1.4 |
Ermitteln Sie die Asymptotengleichung! |
| 1.5 |
Untersuchen Sie die Funktion f im Unendlichen! |
| 1.6 |
Zeichnen Sie den Graph von f in ein geeignetes Koordinatensystem! Die Berechnung weniger weiterer Punkte ist zu empfehlen. Zeichnen Sie die Asymptotengleichung in dasselbe Koordinatensystem ein! |
| 1.7 |
Der Graph der Funktion, die Gerade y = g(x) = x + 2 , und die Parallelen zur y - Achse mit x = 2 und x = 6 begrenzen eine Fläche vollständig. Berechnen Sie den Inhalt dieser Fläche!
|
( Hinweis: |
Verwenden Sie die Darstellung der Funktion f als Summe einer ganzrationalen und einer gebrochenrationalen Funktion - siehe auch 1.4 ! ) |
|
| 2 |
Gegeben sind die Punkte A ( 2 ; -3 ; 5 ) und B ( 1 ; 2 ; -1 ). |
| 2.1 |
Ermitteln Sie eine Gleichung der Geraden g1 durch die Punkte A und B! |
| 2.2 |
Untersuchen Sie die Lagebeziehung zwischen der Geraden g1 und der
|
Geraden g2
|
| ! Berechnen Sie gegebenenfalls den Schnittpunkt ! |
|
| 2.3 |
Bestimmen Sie den Winkel zwischen den Ortsvektoren zu den Punkten A und B! |
| Wahlaufgaben (Von diesen Aufgaben muß nur eine gelöst werden) |
| 3 |
Die Funktion F sei mit y = 2x  e-0,25x² eine Stammfunktion von y = f(x). e-0,25x² eine Stammfunktion von y = f(x). |
| 3.1 |
Ermitteln Sie die Funktionsgleichung f(x)! |
| 3.2 |
Die Funktion f besitzt drei lokale Extrempunkte.
Berechnen Sie die Koordinaten dieser Punkte! (einschließlich Nachweise!) |
| 3.3 |
Zeichnen Sie den prinzipiellen Verlauf des Graphen von f !
Berücksichtigen Sie dabei auch die Nullstellen x1 = - 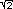 , x2 = , x2 = 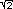 ! ! |
| 3.4 |
Die Graph von f und die x - Achse begrenzen eine Fläche vollständig.
Berechnen Sie deren Inhalt! |
| 4 |
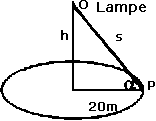
Ein kreisförmiger Straßenplatz mit einem Radius von 20m soll von der Mitte aus so beleuchtet werden, daß der Rand des Platzes möglichst hell wird.
Für die Lichtstärke I in einem Randpunkt gilt:
I = k  |
sin  |
| s2 |
|
| ; k - Konstante |
 |
|
| 4.1 |
Beschreiben Sie die Lichtstärke I als Funktion I = f( ), die als unabhängige Variable nur noch den Winkel ), die als unabhängige Variable nur noch den Winkel  enthält! (siehe Skizze) enthält! (siehe Skizze) |
| 4.2 |
Wie groß muß dieser Winkel sein, damit die Lichtstärke maximal wird? (Auf den Nachweis des Extremums wird verzichtet!) |
| 4.3 |
Ermitteln Sie die Höhe h für diesen Fall! |
 |
|
|
 |
| Prüfung |
 |
| Pflichtaufgaben |
| 1 |
| Die Gleichung y = fa(x) = |
|
- |
|
- 2 x  R , x ≠ 0 ; a R , x ≠ 0 ; a  R , a ≥ 0 R , a ≥ 0 |
beschreibt eine Kurvenschar. Ihre Graphen werden Ka bezeichnet. Diese besitzen an der Stelle x0 eine Polstelle.
|
| 1.1 |
Untersuchen Sie die Funktionen auf Schnittpunkte mit der x - Achse und geben Sie diese in Abhängigkeit von a an ! (Beachten Sie: a = 0, a > 0) |
| 1.2 |
Ermitteln Sie nun die Koordinaten des Extrempunktes von Ka (Nachweis!) und auch die Koordinaten des Wendepunktes von Ka (ohne Nachweis) jeweils in Abhängigkeit von a! |
| 1.3 |
Untersuchen Sie die Funktionen im Unendlichen! Deuten Sie das Ergebnis geometrisch! |
| 1.4 |
Setzen Sie a = 4!
Zeichnen Sie K4 in ein Koordinatensystem im Intervall -6 ≤ x ≤ 6 ! (1 LE = 1cm) |
| 1.5 |
Zeichnen Sie in dasselbe Koordinatensystem die Parallelen zur y-Achse durch x = 1 und x = 4 und die Gerade y = -2! Die Parallelen zur y-Achse, die Gerade y = -2 und der Graph K4 begrenzen eine Fläche vollständig. Berechnen Sie den Inhalt dieser Fläche! |
| 2 |
Zwei Wandergruppen A und B befinden sich zum Zeitpunkt t = 0 in den Punkten A0 (0;0) bzw. B0 (25;0). Siehe Skizze (nicht maßstäblich!) (Koordinateneinheit : 1 km)

Die Gruppe A wandert mit konstanter Geschwindigkeit vA = 3km/h,
die Gruppe B wandert mit konstanter Geschwindigkeit vB = 5km/h. (vgl. Skizze) |
| 2.1 |
Wie lauten die Standortkoordinaten der beiden Gruppen nach 2 Stunden? |
| 2.2 |
Berechnen Sie, wie weit die Wandergruppen nach 2 Stunden voneinander entfernt sind! |
| 2.3 |
Nach wieviel Stunden haben die beiden Gruppen die geringste Entfernung voneinander?
(Auf den Nachweis wird verzichtet!) |
| Wahlaufgaben (Von diesen Aufgaben muß nur eine gelöst werden) |
| 3 |
In einem kartesischen Koordinatensystem sind die Punkte A (4 ; -2), B (8 ; 6) und C (1 ; 4) gegeben. |
| 3.1 |
Geben Sie für die Geraden durch die Punkte A und B, A und C, sowie durch B und C je eine Gleichung in der vektoriellen Form und in der kartesischen Normalform an! |
| 3.2 |
Berechnen Sie die Innenwinkel des Dreiecks ABC! |
| 3.3 |
Ermitteln Sie die Koordinaten des Schwerpunktes S des Dreiecks! |
| 3.4 |
Bestimmen Sie die Koordinaten des Fußpunktes L der Höhe hc auf der Seite 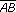 ! ! |
| 4 |
Die Funktion f sei mit y = f(x) = 2  cos2 x + sin x ; 0 ≤ x ≤ 2 cos2 x + sin x ; 0 ≤ x ≤ 2 gegeben. gegeben. |
| 4.1 |
Untersuchen Sie die Funktion f auf Schnittstellen mit der x - Achse und geben Sie diese an! |
| 4.2 |
Berechnen Sie die Extrempunkte von f und weisen Sie deren Art nach! |
| 4.3 |
Skizzieren Sie den Graph von f im vorgegebenen Intervall! |
| 4.4 |
Weisen Sie nach, dass die Funktion F: F(x) = x + 0,5  sin 2x - cos x sin 2x - cos x
eine Stammfunktion von f ist! |
 |
|
|
 |
| Prüfung |

 |
| Pflichtaufgaben |
| 1 |
Gegeben ist die Funktion f mit y = f(x) = 10  e-x e-x  ( -2x2 + 8x - 4 ). ( -2x2 + 8x - 4 ).
|
| 1.1 |
Berechnen Sie die Nullstellen dieser Funktion! |
| 1.2 |
Berechnen Sie die Koordinaten der Extrempunkte und prüfen Sie die hinreichenden Bedingungen für Hoch- bzw. Tiefpunkte! |
| 1.3 |
Ermitteln Sie die Koordinaten von Wendepunkten und prüfen Sie jeweils die diesbezügliche hinreichende Bedingung! |
| 1.4 |
Skizzieren Sie den Graph von f im Intervall [ 0,5 ; 8 ]! |
| 1.5 |
Weisen Sie nach, dass die Funktion F mit F(x) = 10  ( 2x2 - 4x ) ( 2x2 - 4x )  e-x eine Stammfunktion von f ist und berechnen Sie den Inhalt der Fläche, die von der x - Achse und vom Graph von f im ersten Quadranten eingeschlossen wird! e-x eine Stammfunktion von f ist und berechnen Sie den Inhalt der Fläche, die von der x - Achse und vom Graph von f im ersten Quadranten eingeschlossen wird! |
| 2 |
Für ein neues Kinderspiel wurden vielfältige neue Bausteinformen entwickelt, unter anderem Kugeln, in die die Form eines Zylinders einbeschrieben ist.
Zur Realisierung dieser Aufgabe ist es notwendig, Grundkreisradius r, Höhe h und das größtmögliche Volumen V des Zylinders, der sich in eine Kugel mit gegebenen Radius R einbeschreiben läßt, zu bestimmen. |
| Wahlaufgaben (Von diesen Aufgaben muß nur eine gelöst werden) |
| 3 |
Durch die Punkte A ( -2 ; 3 ; 4 ) und B ( 1 ; 5 ; 2 ) sowie durch A und C ( 4 ; -3 ; 1 ) verlaufen jeweils Geraden. |
| 3.1 |
Wie lauten die Gleichungen der beiden Geraden? |
| 3.2 |
Ermitteln Sie die Punkte D und E, die jeweils einen Abstand von 20 Einheiten auf den obrigen Geraden von A in Richtung B bzw. von A in Richtung C besitzen! |
| 3.3 |
Bestimmen Sie den Winkel zwischen den Geraden! |
| 4 |
Gegeben ist die Funktion f mit y = f(x) = sin2x - 2  sin x ; 0 ≤ x ≤ 2 sin x ; 0 ≤ x ≤ 2 |
| 4.1 |
Untersuchen Sie die Funktion f auf Schnittstellen mit der x-Achse und geben Sie diese an! |
| 4.2 |
Berechnen Sie die Extrempunkte und weisen Sie deren Art nach! |
| 4.3 |
Skizzieren Sie den Graph von f im vorgegebenen Intervall! |
| 4.4 |
Berechnen Sie den Inhalt der Flächen, die vom Graph der Funktion f und der x - Achse im Intervall eingeschlossen werden. |
 |
|
|

 |
| Prüfung |
 |
| Pflichtaufgaben |
| 1 |
| Die Gleichung y = f(x) = |
|
; x ≠ 0 beschreibt eine Schar von Funktionen fa. |
Ihre Graphen werden mit Ka bezeichnet.
|
| 1.1 |
| Untersuchen Sie fa |
für |
a > 0, |
|
| |
für |
a = 0 |
|
| |
und für |
a < 0 |
auf Nullstellen. Begründen Sie Ihre Entscheidung! |
|
| 1.2 |
Weisen Sie durch Rechnung nach, dass yA = 2x die Asymptotengleichung für alle Graphen von fa ist! |
| 1.3 |
Es sei nun a > 0 vorausgesetzt. Berechnen Sie die lokalen Extremstellen unter dieser Voraussetzung und weisen Sie deren Art nach! |
| 1.4 |
Setzen Sie nun a = 4!
Schreiben Sie jetzt die entsprechende Funktionsgleichung für f4 auf und ermitteln Sie unter Nutzung der vorliegenden Ergebnisse die Koordinaten der Extrempunkte von f4!
Ermitteln Sie ggf. noch weitere Punkte!
Zeichnen Sie in ein gemeinsames Koordinatensystem die Asymptote ein und den Graph der Funktion f4, außerdem die Parallele zur x-Achse y = 9. |
| 1.5 |
Die Parallele zur x-Achse y = 9 schneidet den Graph von f4 im I.Quadranten in zwei Punkten. Berechnen Sie die Schnittpunktkoordinaten! |
| 1.6 |
Der Graph K4 und die Gerade y = 9 begrenzen im I.Quadranten eine endliche Fläche.
Berechnen Sie deren Inhalt! |
| 2 |
Kraft 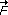 und Hebelarm und Hebelarm 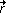 sind durch die Vektoren sind durch die Vektoren 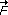 = (100;150;200)N und = (100;150;200)N und 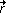 = ( 0,3;0,1;0,2 )m gegeben. = ( 0,3;0,1;0,2 )m gegeben.
(Hinweis: Der physikalische Charakter der gegebenen Vektoren ist für die Lösung der Aufgabe ohne Belang!)
Berechnen Sie: |
| 2.1 |
den Winkel  zwischen zwischen 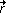 und und 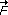 , , |
| 2.2 |
den Anteil  der Kraft der Kraft  , der rechtwinklig zum Hebelarm , der rechtwinklig zum Hebelarm 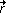 wirkt und den Vektor wirkt und den Vektor 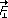 in Koordinatenform, in Koordinatenform, |
| 2.3 |
das Drehmoment 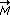 = = 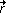  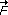 sowie dessen Betrag! sowie dessen Betrag! |
| Wahlaufgaben (Von diesen Aufgaben muß nur eine gelöst werden) |
| 3 |
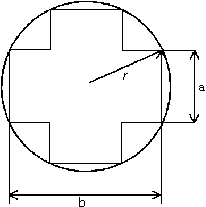 Einen Kreis mit dem Radius r = 4cm soll ein kreuzförmiger Querschnitt Q gleicher "Balkenbreite" einbeschrieben werden (vgl. Skizze). Es ist a < b gegeben.
Einen Kreis mit dem Radius r = 4cm soll ein kreuzförmiger Querschnitt Q gleicher "Balkenbreite" einbeschrieben werden (vgl. Skizze). Es ist a < b gegeben. |
| 3.1 |
Stellen Sie den Flächeninhalt des Querschnitts Q in Abhängigkeit von a und b dar! |
| 3.2 |
Suchen Sie eine Beziehung zwischen a, b und r und stellen Sie diese nach b um! |
| 3.3 |
Der Querschnitt Q ist nun als Q = f(a) anzugeben! |
| 3.4 |
Wie müssen a und b gewählt werden, damit der Flächeninhalt von Q maximal wird? Auf den Nachweis des Extremums wird verzichtet! |
| 4 |
Gegeben sind die Matrizen:
Berechnen Sie aus der folgenden Matrizengleichung die Matrix X!
3AX - 2B = 2CX + 4D
|
 |
|
|
 |
| Prüfung |
 |
| Pflichtaufgaben |
| 1 |
Gegeben ist die Funktion f mit y = f(x) = ( 2x2 + 2x - 4 )  e-0,5x. e-0,5x. |
| 1.1 |
Berechnen Sie die Schnittpunkte des Graphen mit den Koordinatenachsen! |
| 1.2 |
Untersuchen Sie die Funktion f im unendlichen! |
| 1.3 |
Berechnen Sie Extrem- und Wendepunkte *einschließlich Nachweise* ! |
| 1.4 |
Fertigen Sie eine Skizze des Graphen der Funktion im Intervall [ -2 ; 10 ] an! |
| 1.5 |
Zeigen Sie, dass F(x) = ( -4x2 - 20x - 32 )  e-0,5x eine Stammfunktion von f(x) ist! e-0,5x eine Stammfunktion von f(x) ist!
Berechnen Sie die Fläche, die unterhalb der x-Achse vollständig vom Graph f(x) und der x-Achse eingeschlossen wird! |
| 2 |
Aus der Physik ist bekannt
| |
Treffen parallele Lichtstrahlen auf die Innenfläche eines Parabolspiegels, so werden sie zum Brennpunkt hin reflektiert. |
Die Abbildung stellt den Querschnitt eines Parabolspiegels dar, der durch die Gleichung
y = p(x) = 0,125x2 mit dem Brennpunkt F ( 0 ; 2 ) beschrieben wird.
(Die Parabelpunkte P1 und P2 liegen symmetrisch zur y-Achse.)
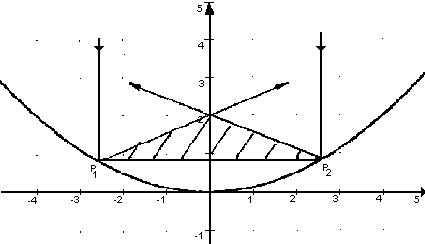 Überlegungen einer technischen Realisierung verlangen, dass die in der Abbildung schraffierte Fläche maximal wird.
Berechnen Sie für diesen Fall die Koordinaten der Punkte
Überlegungen einer technischen Realisierung verlangen, dass die in der Abbildung schraffierte Fläche maximal wird.
Berechnen Sie für diesen Fall die Koordinaten der Punkte
P1 und P2! |
| Wahlaufgaben (Von diesen Aufgaben muß nur eine gelöst werden) |
| 3 |
Es sind die Punkte A( 3; 2; 3 ), B( 1; 5; 1 ), C( 4; 9; 4 ) und D( 6; 6; 8 ) gegeben. |
| 3.1 |
Geben Sie die Vektoren 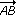 , , 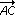 und und 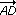 an! an! |
| 3.2 |
Zeigen Sie, dass 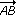 , , 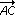 , , 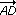 nicht komplanar sind! nicht komplanar sind! |
| 3.3 |
Wie müsste k gewählt werden, damit 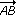 , , 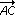 , , 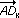 = = |
 |
|
 |
komplanar sind? |
Welche Koordinaten hat dann Dk?
|
| 3.4 |
Zeigen Sie, dass 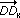 nicht orthogonal zu nicht orthogonal zu 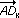 ist! ist! |
| 3.5 |
Berechnen Sie den Inhalt der Dreiecksfläche ABC! |
| 4 |
Gegeben sind die Matrizen:
Lösen Sie die folgende Matrizengleichung: 2A-1X + 3BT = 4X + 2C
|
 |
|
|
 |
|